对象的创建过程
1、JVM遇到一条字节码new指令时
2、检查该指令是否能在常量池中定位到一个类的符号引用,并检查这个符号引用代表的类是否已被加载。
- 2.1、如果没有加载,必须先执行相应的类加载过程。
3、为新生对象分配内存。 - 3.1、 采用哪种垃圾回收器,其内存分配算法是不同的;
- 3.2、 内存分配存在并发问题,一种:采用同步或CAS的方式;第二种:在每个线程中预先分配一小块内存(称为TLAB),只有本地缓冲区用完了,分配新的缓存区时才需要同步锁定。
4、虚拟机必须将分配到的内存空间(不包括对象头)都初始化为零值。
5、JVm还要对对象进行必要的设置,如:该对象是哪个类的实例、类的元数据信息、对象hashcode、对象的GC分带年龄等信息。
对象的内存布局
1、对象头(Header)
- 1.1、第一类用于存储对象自身的运行时数据,如hashcode、GC分代年龄、锁状态标志、线程持有的锁、偏向线程ID、偏向时间戳等。其长度在32-64位的虚拟机中分别为32bit或64bit,官方称为:MarkWord。
- 1.2、第二类是类型指针:对象指向它的类型元数据的指针,JVM通过该指针确定该对象是哪个类的实例。查找对象的元数据信息并不一定要通过对象本身。
2、实例数据(Instance Data)
存储代码中定义的各种类型的字段内容,无论是父类继承的还是子类定义的都记录下来。
3、对齐填充(Padding)
仅起到占位符的作用,对象头是8个字节,实例数据如果没有对齐(不是8个倍数),就需要对齐填充来补全。
对象的访问定位
Java程序通过栈上的reference数据来操作堆上的具体对象,主流访问方式主要有使用句柄和指针两种:
句柄:
Java堆中将可能会划分出来一块内存来作为句柄池,reference中存储的就是对象的句柄地址,而句柄中包含了对象实例数据与类型数据各自具体的地址信息。图2-2
指针:
Java堆中对象的内存布局就必须考虑如何放置访问类型数据的相关信息,reference中存储的直接就是对象地址,如果只访问对象本身,不需要多一次间接访问开销。图2-3
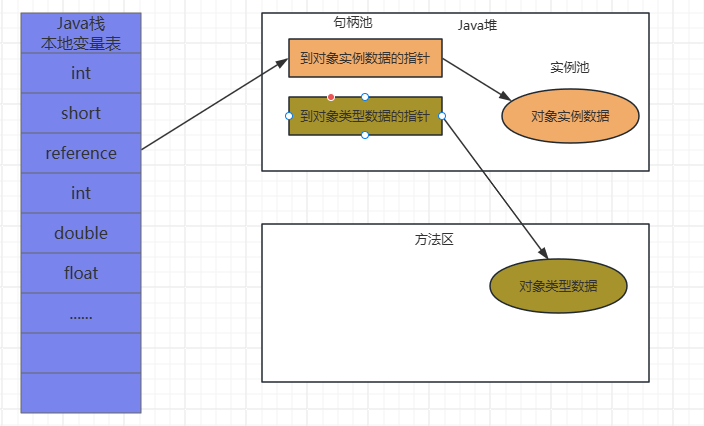
图2-2
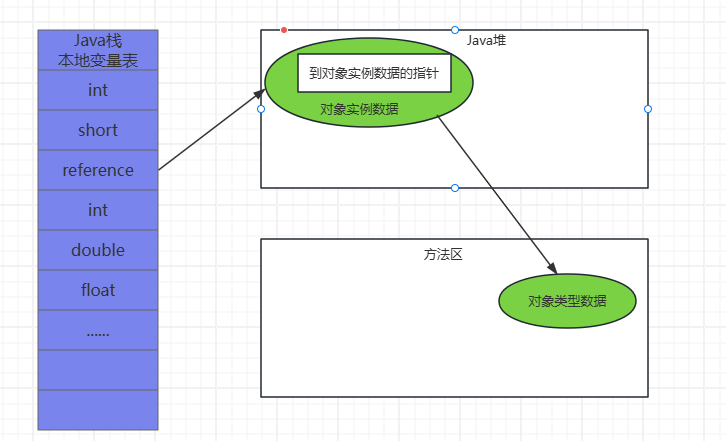
图2-3
