使用PyCharm来实现ArcGisPro的数据批处理,首先需要定位到ArcGisPro的虚拟环境位置。为了防止破坏原始的环境,最好备份一个原环境或者克隆环境到自己熟悉的位置,就可以根据自己的需要在环境里添加自己需要的功能包。比较意外的是ArcGisPro提供克隆功能,不知道和自己手动克隆有什么区别,还是试一下吧。我使用的软件版本为3.1.5。
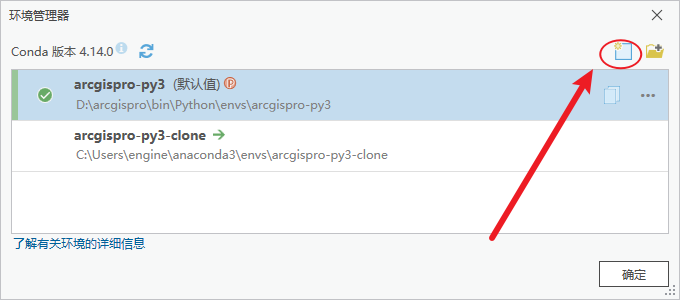
具体的功能路径为:工程→包管理→环境管理器(齿轮状按钮)→克隆环境(类似文本按钮)
使用PyCharm来实现ArcGisPro的数据批处理,首先需要定位到ArcGisPro的虚拟环境位置。为了防止破坏原始的环境,最好备份一个原环境或者克隆环境到自己熟悉的位置,就可以根据自己的需要在环境里添加自己需要的功能包。比较意外的是ArcGisPro提供克隆功能,不知道和自己手动克隆有什么区别,还是试一下吧。我使用的软件版本为3.1.5。
具体的功能路径为:工程→包管理→环境管理器(齿轮状按钮)→克隆环境(类似文本按钮)
