介绍
top命令可以查看各个进程的cpu,内存等所占用的情况,在排查问题当中经常用到。
执行top命令后,默认会出现如下内容:
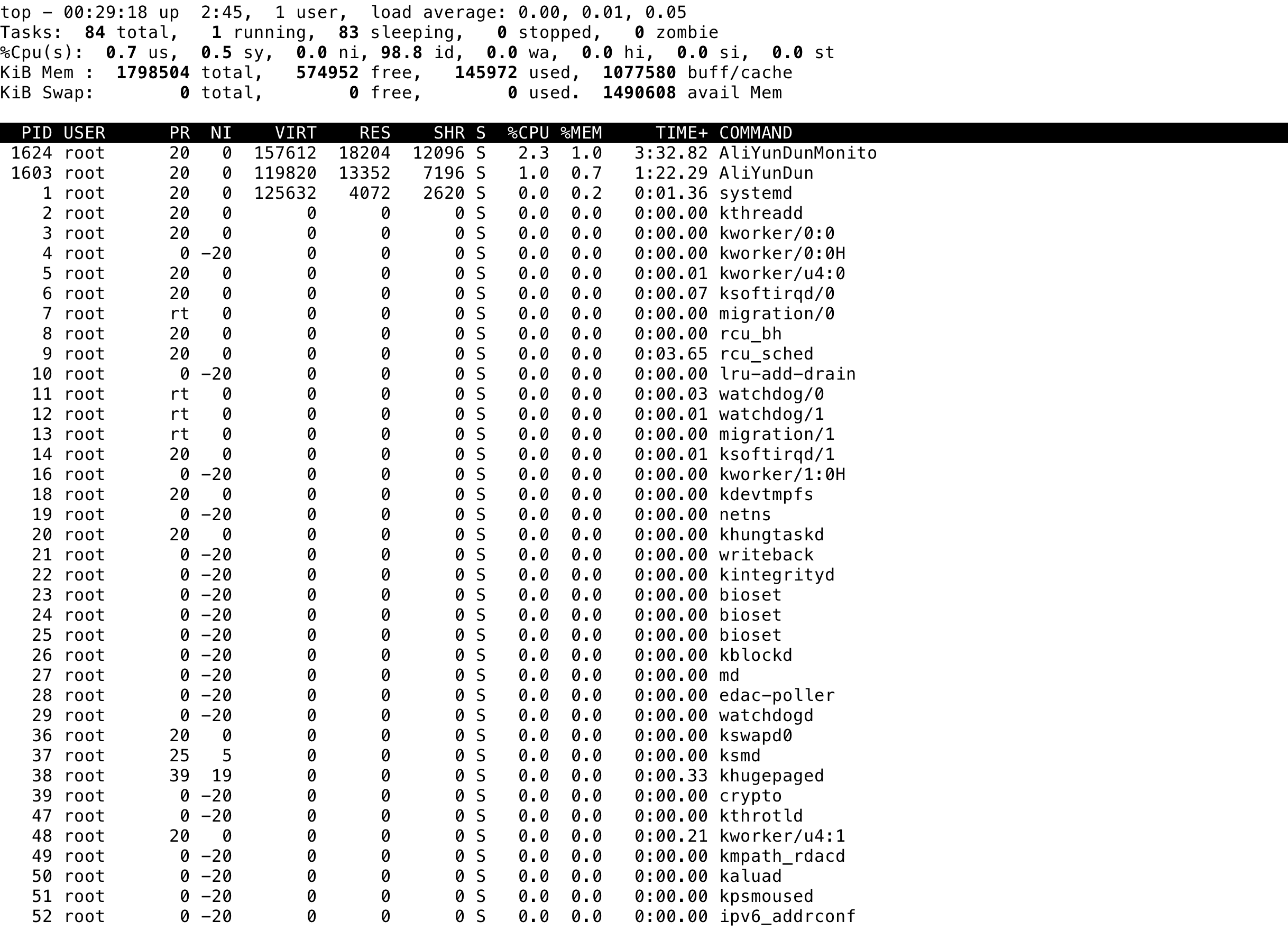
top命令输出了很多参数,真正的服务器负载情况我们要综合其他参数一起看,运行结果可以分为两部分:
- 第一部分是前5行,是系统整体的统计信息;
- 第二部分是第8行开始的进程信息,我们从上往下逐行依次进行说明。
系统整体的统计信息
第一行
top - 00:30:15 up 2:46, 1 user, load average: 0.00, 0.01, 0.05
# top:当前时间。
# up:机器运行了多长时间。
# users:当前登录用户数。
# load average:系统负载,即任务队列的平均长度。三个数值分别为 1分钟、5分钟、15分钟前到现在的平均值。
这里具体需要关注的是load average三个数值。表示在一段时间内,CPU正在处理以及等待CPU处理的进程数之和。三个数字分别代表了1分钟,5分钟,15分钟的统计值,这个数值的确能反应服务器的负载情况。
但是,这个数值高了也并不能直接代表这台机器的性能有问题,可能是因为正在进行CPU密集型的计算,也有可能是因为I/O问题导致运行队列堵了。所以,当我们看到这个数值飙升的时候,还得具体问题具体分析。
大家都知道,一个CPU在一个时间片里面只能运行一个进程,CPU核数的多少直接影响到这台机器在同时间能运行的进程数。所以一般来说Load Average的数值别超过这台机器的总核数,就基本没啥问题。
第二行
Tasks: 84 total, 1 running, 83 sleeping, 0 stopped, 0 zombie
# Tasks:当前有多少进程。
# running:正在运行的进程数。
# sleeping:正在休眠的进程数。
# stopped:停止的进程数。
# zombie:僵尸进程数。
第三行
%Cpu(s): 0.8 us, 0.5 sy, 0.0 ni, 98.7 id, 0.0 wa, 0.0 hi, 0.0 si, 0.0 st
# us:用户空间占CPU的百分比
# sy:内核空间占CPU的百分比
# ni:调整过nice值的进程消耗掉的CPU时间
# id: 空闲CPU占用率。
# wa: 等待输入输出的CPU时间百分比,一般这个值高代表磁盘io较大。
# hi:硬中断占用百分比,硬中断是硬盘、网卡等硬件设备发送给CPU的中断消息,当CPU收到中断消息后需要进行适当的处理(消耗CPU时间)
# si:软中断占用百分比(软中断是由程序发出的中断,最终也会执行相应的处理程序,消耗CPU时间)。
# st:Steal Time(窃取时间) ,当系统运行在虚拟化环境(如虚拟机)中时,物理 CPU 资源被同一物理机上的其他虚拟机占用,导致当前虚拟机无法使用 CPU 的时间比例。
第四行
KiB Mem : 1798504 total, 510160 free, 169572 used, 1118772 buff/cache
# total:物理内存总量。
# free:空闲内存量。
# used:使用的内存量。
# buffer/cache:用作内核缓存的内存量。
第五行
KiB Swap: 0 total, 0 free, 0 used. 1461408 avail Mem
# total:交换区内存总量。
# free:空闲交换区总量。
# used:使用的交换区总量。
# buffer/cache:缓冲的交换区总量。
进程信息
PID USER PR NI VIRT RES SHR S %CPU %MEM TIME+ COMMAND1624 root 20 0 157612 18204 12096 S 2.0 1.0 3:44.32 AliYunDunMonito1603 root 20 0 148488 40856 7196 S 0.7 2.3 1:27.12 AliYunDun1 root 20 0 125632 4072 2620 S 0.0 0.2 0:01.36 systemd2 root 20 0 0 0 0 S 0.0 0.0 0:00.00 kthreadd3 root 20 0 0 0 0 S 0.0 0.0 0:00.00 kworker/0:04 root 0 -20 0 0 0 S 0.0 0.0 0:00.00 kworker/0:0H# PID: 进程id
# USER: 进程所有者的用户名
# PR: 优先级
# NI: nice值,负值表示高优先级,正值表示低优先级
# VIRT: 进程使用的虚拟内存总量,单位kb。VIRT=SWAP+RES
# RES: 代表进程实际使用的物理内存(未被换出到磁盘),单位kb。
# SHR: 共享内存大小,单位kb
# S: 进程状态。D=不可中断的睡眠状态 R=运行 S=睡眠 T=跟踪/停止 Z=僵尸进程
# %CPU: 上次更新到现在的CPU时间占用百分比
# %MEM: 进程使用的物理内存百分比
# TIME+: 进程使用的CPU时间总计,单位1/100秒
# COMMAND: 命令名/命令行
top常用参数
-d: 指定刷新的时间,如希望每秒刷新一次,则使用:top -d 1
-p: 通过指定PID来仅仅监控某个进程的状态
-S: 指定累计模式
-s: 使top命令在安全模式中运行,这将除去交互命令所带来的潜在危险
-H: 输出某个特定进程<pid>并检查该进程内运行的线程状况:top -H -p <pid>
top交互命令使用
通过按f键可以编辑显示内容,按f键后,会出现下图
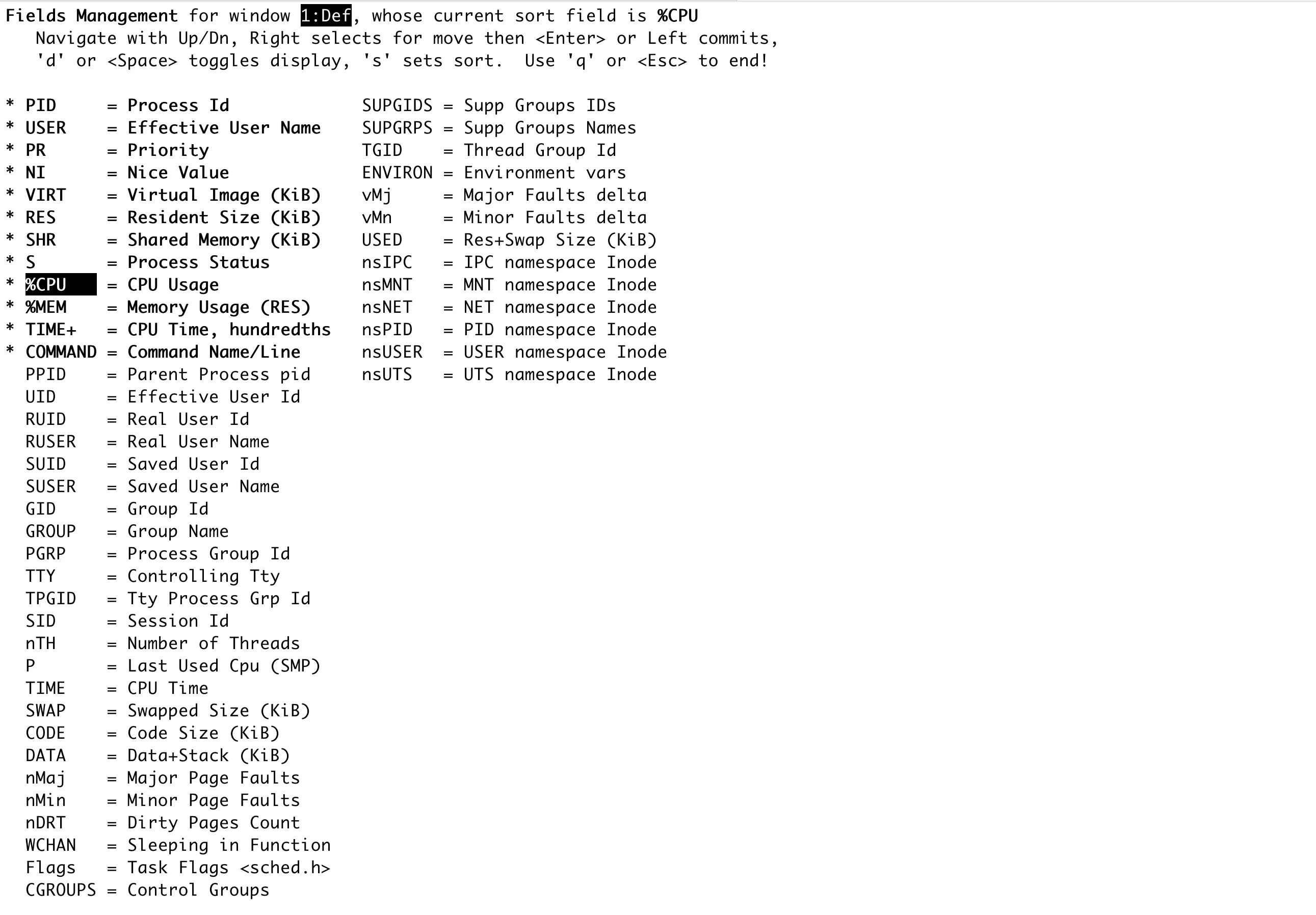
- 当前是按照%CPU这一列来排序的。
- 可以通过上、下键来选择。
- 按右键可以选择整个列,然后按上、下键来移动整个列的显示位置,前移或后移,按回车确定。
- 按空格键来显示或隐藏该列,带的是显示,不带的是不显示。
- 按s键可以将当前列设置为排序列。
- 按q键退出。
快捷键补充:
- 敲top后,按键盘数字“1”可以监控每个逻辑CPU的状况
- 敲top后,输入u,然后输入用户名,则可以查看相应的用户进程
- 敲top后,top命令默认以K为单位显示内存大小,我们可以通过大写字母E来切换内存信息区域的显示单位,如下按一下E切换到MB,再按一下E切换到GB
- 敲top后,输入h进入top命令的帮助文档,了解更多关于top的用法

 top命令的各个参数解释,常用参数以及交互快捷键的使用详解
top命令的各个参数解释,常用参数以及交互快捷键的使用详解