第二章:Linux基础命令
1.Linux的目录结构
Linux操作系统的目录结构
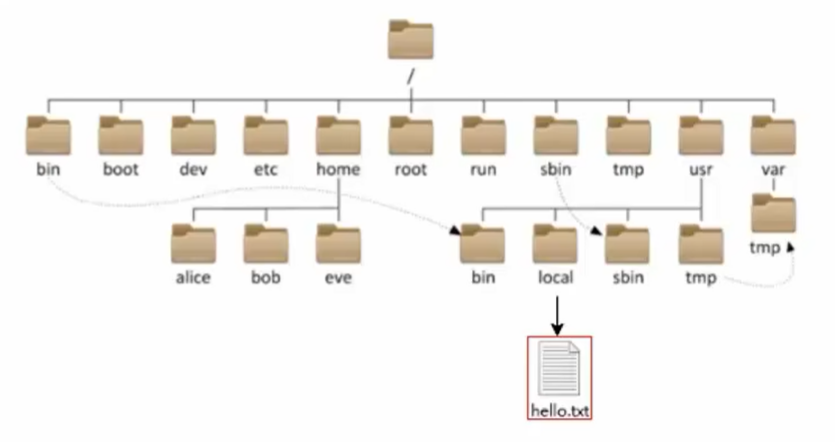
Linux只有一个顶级目录,称为:根目录,用\表示,所有文件都在它下面。

Windows系统有多个顶级目录,即各个盘符,如C盘、D盘、E盘。

/在Linux系统中表示
- 出现在开头的/表示:根目录
- 出现在后面的/表示:层次关系
- /usr/local/hello.txt
![img]()
2.Linux命令入门
Linux命令基础
什么是命令行、命令
- 命令行:即Linux终端(Terminal),是一个命令提示符页面。以纯"字符"的形式操作系统,可以使用各种字符化命令对系统发出操作指令。
- 命令:即Linux操作指令,是系统内置的程序,可以以字符化的形式去使用。
Linux命令基础格式
无论是什么命令,用在什么用途,在Linux中,命令有其通用的格式:
command [options] [parameter]
- comman:命令本身
- optons(可选):命令的一些选项,可以通过选项控制命令的行为细节。
- parameter(可选):命令的参数,多数用于命令的指向目标等。
示例:
ls -l /home/itheima,ls是命令本身,-l是选项,/home/itheima是参数。整个命令意思是以列表的形式,显示/home/itheima目录内的内容。cp -r test1 test2,cp是命令本身,-r是选项,test1和test2是参数。整个命令意思是复制文件夹test1称为test2。
ls命令入门
ls命令的作用
在命令行中,以平铺的形式,展示当前工作目录(默认HOME目录)下的内容(文件或文件夹)。
HOME目录
每一个用户在Linux系统的专属目录,默认在:/home/用户名
当前工作目录
Linux命令在执行命令的时候,需要一个工作目录,打开命令行程序(终端)默认设置工作目录在用户的HOME目录。
ls命令的选项和参数
ls命令格式:
ls [-a -l -h] [Linux路径]
ls选项的作用
-a选项:表示all的意思,及列出全部文件(包括隐藏的文件/文件夹)。
![img]()
-l选项,表示:以列表(竖向排列)的形式展示内容,并展示更多信息,比如权限、用户和用户名、文件大小、创建时间等。
![img]()
-h选项,表示:以易于阅读的形式,列出文件大小,如K、M、G。必须要搭配-l一起使用。
![img]()
- 选项组合运用,
-al、-la、-a-l、-alh、-a-l-h等均可。选项组合的作用是各个选项作用的叠加。
![img]()
ls参数的作用
可以指定要查看的文件夹(目录)的内容,如果不给定参数,就查看当前工作目录的内容。
ls默认查看当前工作目录(HOME目录)。ls /查看根目录的内容。
3.目录切换相关命令(cd/pwd)
cd命令
cd(chage directory)命令的作用是切换当前的工作目录,其语法是:
cd [Linux路径]
- cd命令无需选项,只有参数,表示要切换到哪个目录下。
- cd命令直接执行,不写参数,表示回到用户的HOME目录。
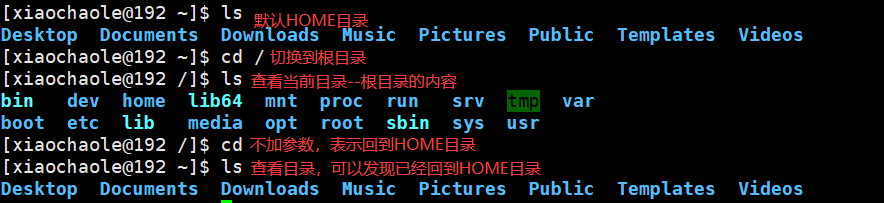
pwd命令
pwd(print work directory)命令的作用是查看当前所在的工作目录的完整路径,其语法是:
pwd
- pwd命令,无选项,无参数,直接输入pwd即可。

4.相对路径、绝对路径和特殊路径
绝对路径、相对路径
- 绝对路径:以根目录为起点,描述路径的一种写法,路径描述以
/开头。
![img]()
- 相对路径:以当前目录为起点,描述路径的一种写法,路径无需以
/开头。
![img]()
特殊路径
.表示当前目录,比如cd ./Desktop表示切换到当前目录下的Desktop目录内,和cd Desktop效果一致。..表示上一级目录,比如cd ..即可切换到上一级目录,cd ../..切换到上二级目录。~表示HOME目录,比如cd ~即可切换到HOME目录或cd ~/Desktop,切换到HOME内的Desktop目录。
5.创建目录命令(mkdir)
mkdir命令
mkdir(make directory)命令的作用是创建新的目录(文件夹),其语法是:
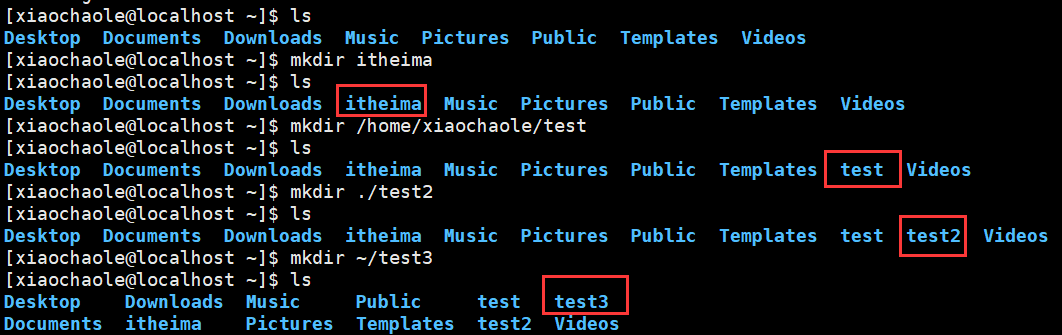
mkdir [-p] Linux路径
- 参数必填,表示Linux路径,即要创建的文件夹的路径,相对路径或绝对路径均可。
![img]()
- -p选项可选,表示自动创建不存在的父目录,适用于创建连续多层级的目录。
![img]()
- 注意:创建文件夹需要修改权限,需要确保操作均在HOME目录内,在HOME目录外操作涉及到权限问题,无法成功创建新的目录。
![img]()
6.文件操作命令part1(touch、cat、more)
touch命令
touch命令用于创建一个新的文件,其语法是:
touch Linux路径
- 参数必填,表示要创建的文件的路径,相对、绝对、特殊路径符都可以使用。
- 以列表形式展开文件目录,可以看出
drwxr-xr-x.表示文件夹,-rw-rw-r--表示文件。
![img]()
cat命令
cat命令用于查看文件内容,其语法是:
cat Linux路径
- 参数必填,表示要查看的文件的路径,相对、绝对、特殊路径符都可以使用。
![img]()
more命令
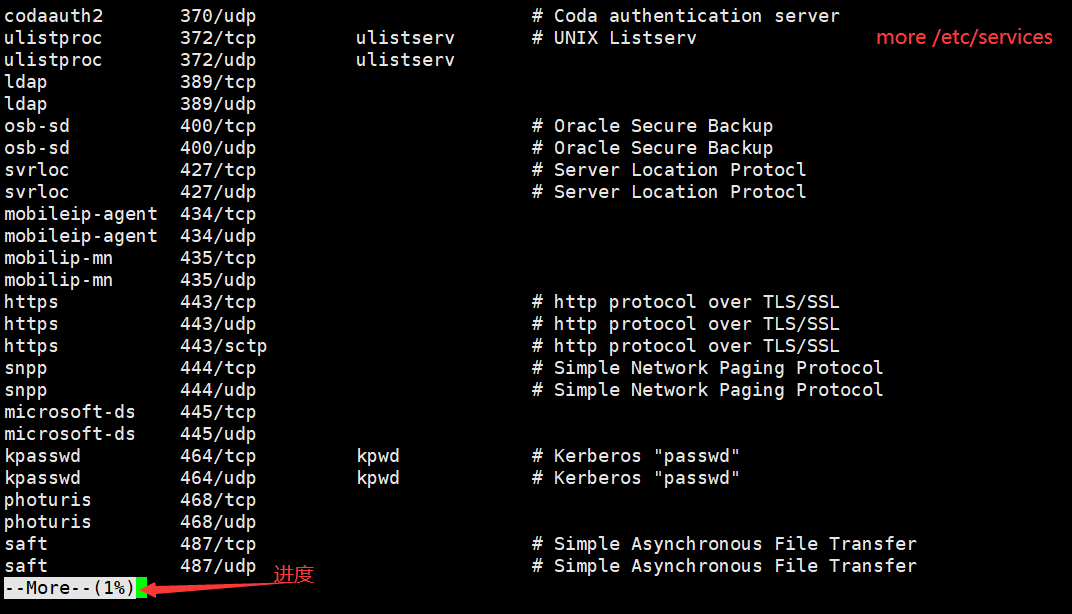
more命令用于查看文件内容,可翻页查看,其语法是:
more Linux路径
- 参数必填,表示要查看的文件的路径,相对、绝对、特殊路径符都可以使用。
- 使用空格键翻下一页,B(back)键翻上一页,Q退出查看。
![img]()
7.文件操作命令part2(cp、mv、rm)
cp命令
cp(copy)命令用于复制文件或文件夹,其语法是:
cp [-r] 参数1 参数2
-r选项,可选,用于复制文件夹。参数1,Linux路径,表示被复制的文件或文件夹。参数2,Linux路径,表示要复制到的地方。
![img]()
mv命令
mv(move)命令用于移动文件或文件夹,其语法是:
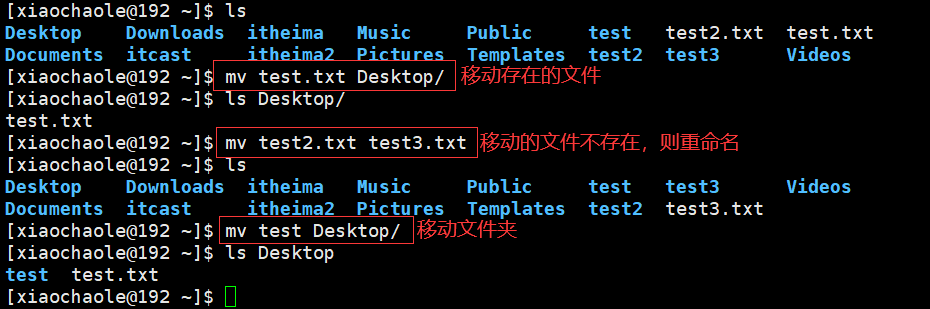
mv 参数1 参数2
参数1,Linux路径,表示被移动的文件或文件夹参数2,Linux路径,表示要移动到的地方,如果目标不存在,则进行改名。
![img]()
rm命令
rm(remove)命令用于删除文件或文件夹,其语法是:
rm [-r -f] 参数1 参数2 ...... 参数N
-r选项,可选,用于删除文件夹。
![img]()
-f选项(force),可选,用于强制删除(一般用于root用户,没有提示信息)- 演示强制删除,通过
su并输入密码,临时切换到root用户体验,演示结束通过exit命令退回普通用户。
![img]()
- 演示强制删除,通过
参数,表述被删除的文件或文件路径,支持多个,用空格隔开。- 参数也支持通配符*,用以做模糊匹配。
- 符号*表示通配符,即匹配任意内容(包括空),示例:
test*,表示匹配任何以test开头的内容。*test,表示匹配任何以test结尾的内容。*test*,表示匹配任何包含test的内容。
![img]()
- rm命令是一个危险的命令,特别是处于root(超级管理员)用户时需谨慎使用。其中
rm -rf /和rm -rf /*不要再root管理员用户下执行,效果相当于在Windows上执行C盘格式化。
8.查找命令(which、find)
which命令
which命令用于查找命令的程序文件的存放位置,其语法是:
which 要查找的命令
- 无需选项,只需要参数表示查找哪个命令。
![img]()
find命令
find命令用于查找指定文件,可以按文件名查找或者按文件大小查找。
按文件名查找
其语法是:
find 起始路径 -name "被查找文件名"
- 在root用户中进行全盘搜索。
![img]()
- 支持使用通配符
*进行模糊查询。
![img]()
按文件大小查找
其语法是:
find 起始路径 -size +/-n[kMG]
- +表示大于,-表示小于。
- n表示大小数字。
- kMG表示大小单位,k(小写字母)表示kb,M表示MB,G表示GB。
![img]()
9.grep、wc和管道符
grep命令
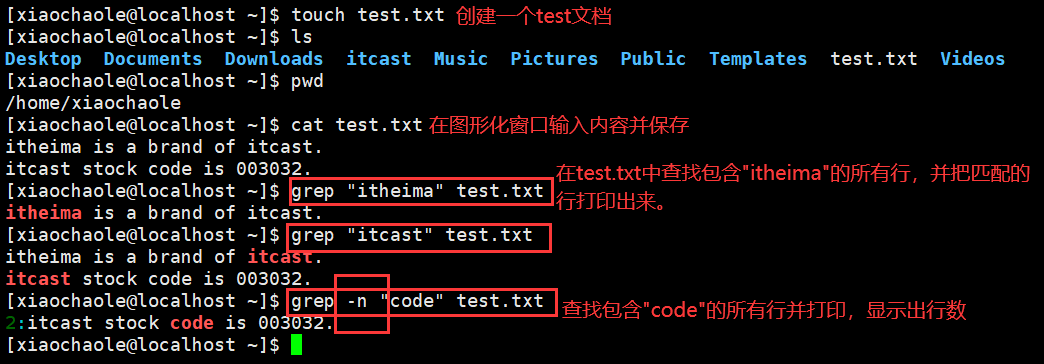
grep命令从文件中查找关键字,并把匹配的行打印出来,其语法是:
grep [-n] 关键字文件路径
- 选项-n,可选,表示在结果中显示匹配的行的行号。
- 参数,关键字,必填,表示要查找的关键字,用" "将关键字包围起来。
- 参数,文件路径,必填,表示要查找内容的文件路径,可作为管道符的输入端口。
![img]()
wc命令
wc命令用于统计文件的字节数、字符数、行数、单词数量等,其语法是:
wc [-c -m -l -w] 文件路径
- 选项-c、-m、-l、-w,可选,-c表示统计字节数,-m表示统计字符数,-l表示统计行数,-w表示统计单词数量。
- 参数,被通缉的文件路径,可作为管道符的输入端口。
![img]()
管道符
管道符的作用是将管道符左边命令的结果,作为右边命令的输入。

10.echo、重定向符和tail
echo命令
echo命令用于在命令行输出指定内容,其语法是:
echo "输出的内容"
- 无需选项,只有一个参数,表示要输出的内容。
- 反引号符,被`包围的内容,会被作为命令执行,而非普通字符。
![img]()
重定向符
>,将左侧命令的结果,覆盖写入到符号右侧指定文件中。>>,将左侧命令的结果,追加写入到符号右侧指定的文件中。
![img]()
tail命令
tail命令用于查看文件尾部内容,并可以持续跟踪,其语法是:
tail [-f -num] Linux路径
- 选项-num,表示查看尾部多少行,不填默认10行。
![img]()
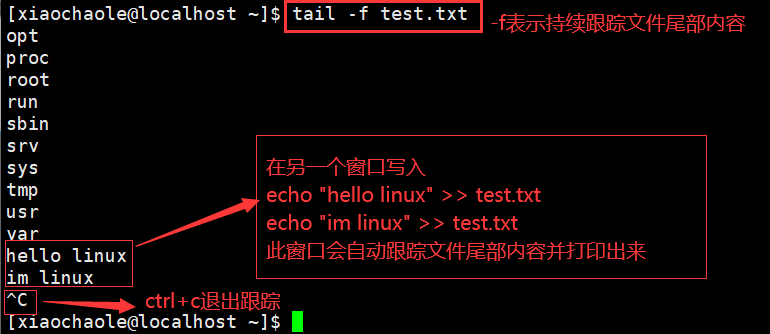
- 选项-f,表示持续跟踪。
- 参数Linux路径,表示被跟踪的文件路径。
![img]()
11.vi\vim编辑器
vi\vim是visual interface的简称,是Linux中最经典的文本编辑器。同图形化界面中的文本编辑器一样,vi是命令行下对文本文件进行编辑的绝佳选择。
什么是vi/vim编辑器
- vi\vim编辑器,就是命令行模式下的文本编辑器,用来编辑文件
- vim是vi的升级版,一般用vim即可,包含全部vi功能。
基础命令
vi 文件路径
vim 文件路径
- 如果文件路径表示的文件不存在,那么此命令会用于编辑新文件。
- 如果文件路径表示的文件存在,那么此命令用于编辑已有文件。
运行模式
1.命令模式
命令模式下,所敲的按键编辑器都理解为命令,以命令驱动执行不同的功能。此模式下,不能自由进行文本编辑。
2.输入模式
输入模式也就是编辑模式、插入模式,通过命令模式进入,可以输入内容进行自由编辑,按esc退回命令模式。
3.底线命令模式
底线命令模式,通过命令模式进入,可以对文件进行保存、关闭等操作。

运行示例
- 在Xshell窗口输入
vim hello.txt,编辑一个新文件,执行后进入的是命令模式。 - 在命令模式内,按键盘i,进入输入模式。
- 在输入模式内输入内容。
![img]()
- 输入完成后,按esc回退回命令模式。
- 在命令模式内,按
:,进入底线命令模式。 - 在底线命令内输入
wq并回车,保存文件并退出vim编辑器。
![img]()
快捷键
命令模式快捷键
| 模式 | 命令 | 描述 |
|---|---|---|
| 命令模式 | i | 在当前光标位置,进入输入模式 |
| 命令模式 | a | 在当前光标位置之后,进入输入模式 |
| 命令模式 | I | 在当前行的开头,进入输入模式 |
| 命令模式 | A | 在当前行的结尾,进入输入模式 |
| 命令模式 | o | 在当前光标下一行,进入输入模式 |
| 命令模式 | O | 在当前光标上一行,进入输入模式 |
| 命令模式 | 键盘上、键盘k | 向上移动光标 |
| 命令模式 | 键盘下、键盘j | 向下移动光标 |
| 命令模式 | 键盘左、键盘h | 向左移动光标 |
| 命令模式 | 键盘右、键盘l | 向后移动光标 |
| 命令模式 | 0 | 移动光标到当前行的开头 |
| 命令模式 | $ | 移动光标到当前行的结尾 |
| 命令模式 | pageup(PGUp) | 向上翻页 |
| 命令模式 | pagedown(PgDn) | 向下翻页 |
| 命令模式 | / | 进入搜索模式 |
| 命令模式 | n | 向下继续搜索 |
| 命令模式 | N | 向上继续搜索 |
| 命令模式 | dd | 删除光标所在行的内容 |
| 命令模式 | ndd | n是数字,表示删除当前光标向下n行 |
| 命令模式 | yy | 复制当前行 |
| 命令模式 | nyy | n是数字,复制当前行和下面的n行 |
| 命令模式 | p | 粘贴复制的内容 |
| 命令模式 | u | 撤销修改 |
| 命令模式 | ctrl + r | 反向撤销修改 |
| 命令模式 | gg | 跳到首行 |
| 命令模式 | G | 跳到行尾 |
| 命令模式 | dG | 从当前行开始,向下全部删除 |
| 命令模式 | dgg | 从当前行开始,向上全部删除 |
| 命令模式 | d$ | 从当前光标开始,删除到本行的结尾 |
| 命令模式 | d0 | 从当前光标开始,删除到本行的开头 |
输入模式快捷键
| 模式 | 命令 | 描述 |
|---|---|---|
| 输入模式 | esc | 任何情况下输入esc都能回到命令模式 |
底线命令模式快捷键
| 模式 | 命令 | 描述 |
|---|---|---|
| 底线命令模式 | :wq | 保存并退出 |
| 底线命令模式 | :q | 仅退出 |
| 底线命令模式 | :q! | 强制退出 |
| 底线命令模式 | :w | 仅保存 |
| 底线命令模式 | :set nu | 显示行号 |
| 底线命令模式 | :set paste | 设置粘贴模式 |