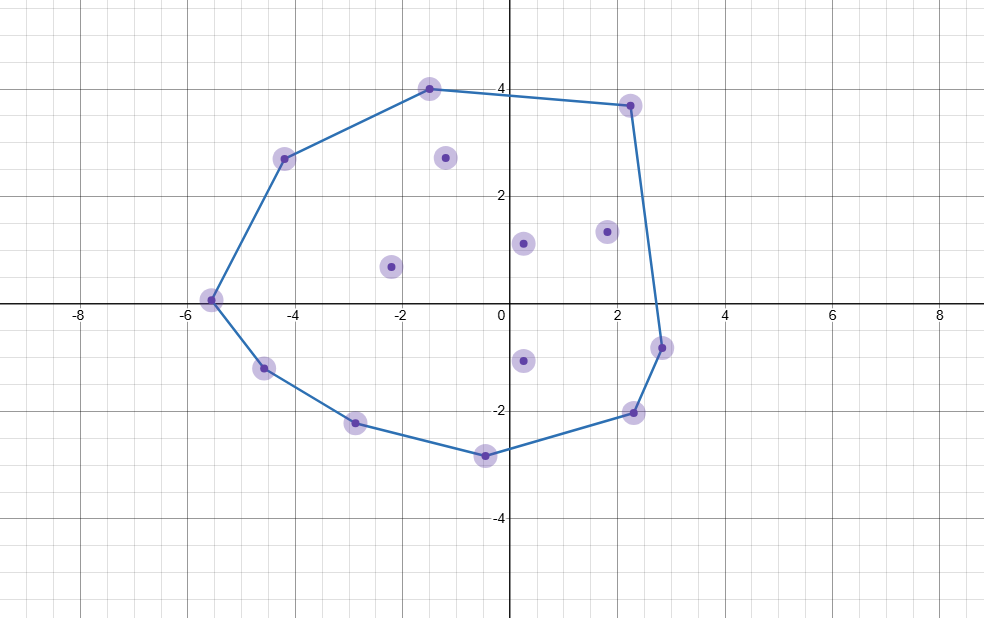
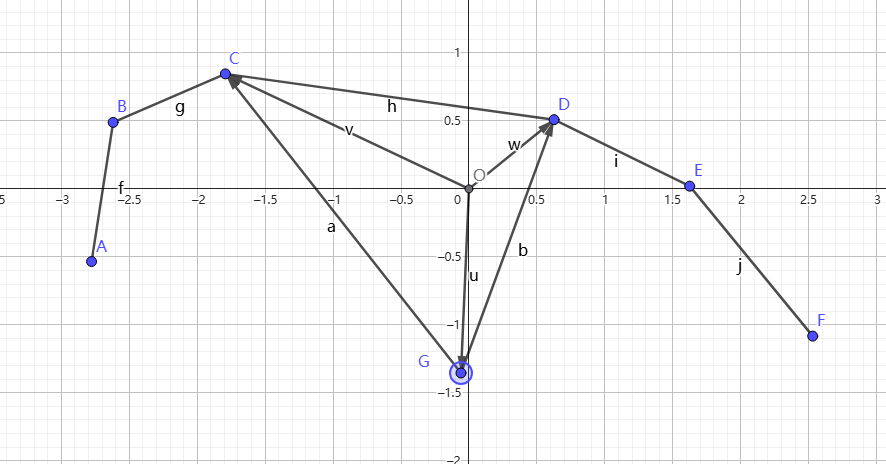
动态凸包概述
动态凸包（Dynamic Convex Hull）问题是指在二维平面上，维护一个点集的凸包结构，并支持在点集中动态地插入或删除点，同时能够高效地查询当前凸包的状态或属性（如周长、面积、顶点集合等）。该问题在计算几何、计算机图形学、机器人路径规划、动态规划等领域具有广泛应用。
前置知识
向量
先看 百度百科 & io-wiki。
定义 1
向量向量顾名思义是具有方向（向）和大小（量）的量，通常使用有向线段（带箭头的线段）表示，如下图：
表示
向量有三种表示方法，如下图的向量：
其可表示为：
- \(\vec a\)；
- \(\vec{AB}\)；
- \((-2.5,1)\)。
其中第三种被称为向量的坐标表示。向量的坐标为终点坐标减起点坐标。
定义 2
如两向量方向相反称这两向量互为相反向量记作 \(\vec v = - \vec u\)。
运算
加减
向量的加法可以看成是一段连续位移的叠加，如图：
其中 \(\vec v + \vec u = \vec w\)，这种加法法则被称为三角形法则。
由此引申可得平行四边形法则，如图：
其中 \(\vec v \mathop{//} f, \vec u \mathop{//} g, \vec v + \vec u = \vec w\)。
向量的减法可以看作加法的逆运算，例如 \(\vec v - \vec u = \vec w\) 表示从 \(\vec v\) 中减去 \(\vec u\) 的效果，等价于 \(\vec v + (-\vec u)\)。
容易得到向量加减的坐标运算为 \((x,y)\pm(a,b)=(x\pm a,y\pm b)\)。
模
向量模为向量的长度，符号与绝对值相同，如图：其中 \(\left | \vec u \right | = \frac{\sqrt{29}}{2}\)。
容易得到向量的模的坐标运算为 \(\left | (a,b) \right | = \sqrt{a^2+b^2}\)。
定义 3
模为 \(1\) 的向量为单位向量，一般用 \(\vec e\) 表示。
叉乘
在二维空间中，向量的叉乘表示两个向量构成的平行四边形的有向面积，如图：
其中 \(\vec w \times \vec v = S_a = -2.25\)。可以得到 \(\vec w \times \vec v = |w||v|\sin<w,v>\)。
可以得到叉乘的坐标运算为 \((a,b)\times(x,y)=ay-bx\)。
证明：
设 \(x\) 轴的单位向量为 \(\vec e_1\)，\(y\) 轴的为 \(\vec e_2\)。\((a,b)\times(x,y) = (a\vec e_1 + b\vec e_2)\times(x\vec e_1 + y\vec e_2)\)。
展开得 \(a x \vec e_1 \times \vec e_1 + a y \vec e_1 \times \vec e_2 + b x \vec e_2 \times \vec e_1 + b y \vec e_2 \times \vec e_2\)。
由于 \(\vec e_1 \times \vec e_1 = 0\)，\(\vec e_2 \times \vec e_2 = 0\)，且 \(\vec e_1 \times \vec e_2 = -\vec e_2 \times \vec e_1 = 1\)（\(\vec e_1\perp\vec e_2\)）。
化简得 \(a y - b x\)，得证。
叉乘符号则表示两个向量的相对方向关系：
- 若结果为正，表示第二个向量在第一个向量的逆时针方向；
- 若结果为负，表示第二个向量在第一个向量的顺时针方向；
- 若结果为 0，说明两向量共线。
凸包
先看 百度百科 &oi-wiki。
定义一
在平面上能包含所有给定点的最小凸多边形叫做凸包。
如图：
其中蓝色多边形为凸包：
实际上可以理解为用一个橡皮筋包含住所有给定点的形态。
定义二
凸包中相邻的边若斜率愈来愈大则称下凸壳，相邻的边若斜率愈来愈小称上凸壳。
Andrew's Monotone Chain 算法
以下来自 oi-wiki。
该算法的时间复杂度为 \(O(n \log n)\)，其中 \(n\) 为待求凸包点集的大小。复杂度的瓶颈在于对所有点坐标的双关键字排序。
具体过程如下：
- 排序：
将所有点以横坐标为第一关键字、纵坐标为第二关键字进行升序排序。排序后，最小和最大的元素一定在凸包上。 - 构造凸壳：
利用单调栈维护凸壳。由于上下凸壳旋转方向不同，先升序枚举构造下凸壳，再降序枚举构造上凸壳。 - 判断方向：
从栈顶取出两个点 \(S_1\)、\(S_2\)（其中 \(S_1\) 为栈顶），若即将入栈的点 \(P\) 与这两个点构成的方向为右拐（即叉积小于 0）：\(\vec{S_2S_1} \times \vec{S_1P} < 0\) 则弹出栈顶 \(S_1\)，重复此过程直到满足：\(\vec{S_2S_1} \times \vec{S_1P} \leq 0\) 或栈中只剩一个元素为止。 - 保留边界点（可选）：
若需保留凸包边界上的点，可将上述条件中的<改为≤，相应地将反向判断条件>改为≥。
最终将上下凸壳合并，即可得到完整的凸包。
code
点击查看代码
// stk[] 是整型，存的是下标
// p[] 存储向量或点
tp = 0; // 初始化栈
std::sort(p + 1, p + 1 + n); // 对点进行排序
stk[++tp] = 1;
// 栈内添加第一个元素，且不更新 used，使得 1 在最后封闭凸包时也对单调栈更新
for (int i = 2; i <= n; ++i) {while (tp >= 2 // 下一行 * 操作符被重载为叉积&& (p[stk[tp]] - p[stk[tp - 1]]) * (p[i] - p[stk[tp]]) <= 0)used[stk[tp--]] = 0;used[i] = 1; // used 表示在凸壳上stk[++tp] = i;
}
int tmp = tp; // tmp 表示下凸壳大小
for (int i = n - 1; i > 0; --i)if (!used[i]) {// ↓求上凸壳时不影响下凸壳while (tp > tmp && (p[stk[tp]] - p[stk[tp - 1]]) * (p[i] - p[stk[tp]]) <= 0)used[stk[tp--]] = 0;used[i] = 1;stk[++tp] = i;}
for (int i = 1; i <= tp; ++i) // 复制到新数组中去h[i] = p[stk[i]];
int ans = tp - 1;
正文 —— Andrew's Monotone Chain 算法变种
现在考虑已经有一个凸壳（为了方便讲解，以上凸壳为例），如下图：
现在考虑插入一个点，分两种情况讨论：
情况一：点在凸包下或在凸包上
如图：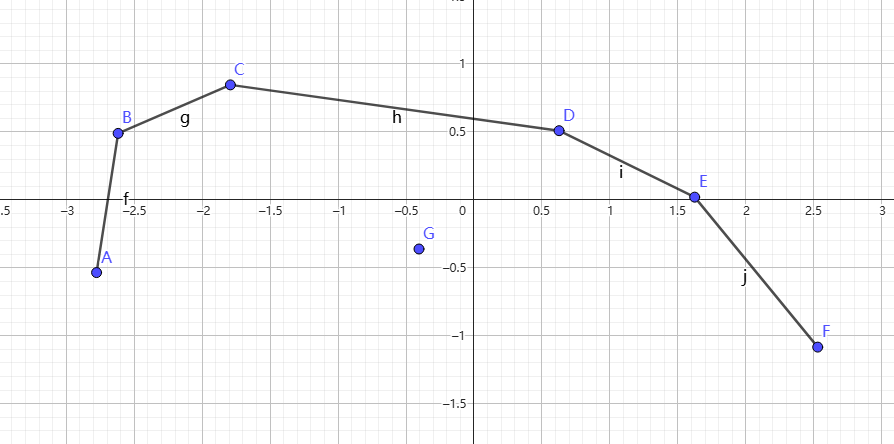
证明：根据向量叉乘的几何意义，\(\vec{GC} \times \vec{GD}\) 的结果表示以 \(GC\) 和 \(GD\) 为邻边的平行四边形的有向面积。若该值 \(\leq 0\)，则说明向量 \(\vec{GD}\) 位于向量 \(\vec{GC}\) 的顺时针方向或共线。
设 \(C\)、\(D\) 为插入点 \(G\) 在凸包中的前驱和后继（按 \(x\) 坐标排序），则凸包上 \(C\) 到 \(D\) 的线段是上凸壳的一部分，其斜率单调递减（上凸壳的性质）。若 \(G\) 在凸包下方或凸包上，则 \(G\) 必须位于线段 \(CD\) 的下方或线段上。此时，线段 \(GC\) 的斜率 \(k_1\) 必然大于等于线段 \(GD\) 的斜率 \(k_2\)（即 \(k_1 \geq k_2\)），否则 \(G\) 会位于凸包外部，导致原凸包不再是“最小凸多边形”。
根据叉乘的坐标运算：
设 \(G(x_0,y_0)\)，\(C(x_1,y_1)\)，\(D(x_2,y_2)\)，则：\(\vec{GC} = (x_1-x_0, y_1-y_0)\)，\(\vec{GD} = (x_2-x_0, y_2-y_0)\)，\(\vec{GC} \times \vec{GD} = (x_1-x_0)(y_2-y_0) - (x_2-x_0)(y_1-y_0)\)
若 \(k_1 \geq k_2\)，即 \(\frac{y_1-y_0}{x_1-x_0} \geq \frac{y_2-y_0}{x_2-x_0}\)（假设 \(x_1 < x_0 < x_2\)，分母为正），交叉相乘得：\((y_1-y_0)(x_2-x_0) \geq (y_2-y_0)(x_1-x_0)\)
移项后：\((x_1-x_0)(y_2-y_0) - (x_2-x_0)(y_1-y_0) \leq 0\)
即 \(\vec{GC} \times \vec{GD} \leq 0\)。
此时容易发现，这个点不可能改变凸壳。