传送门
标签:思维题、计算几何。
思路
显然给了极坐标是有含义的,没有必要转换。
先想暴力,如何计算一个单位圆内接三角形的面积?
显然,我们可以这样算:
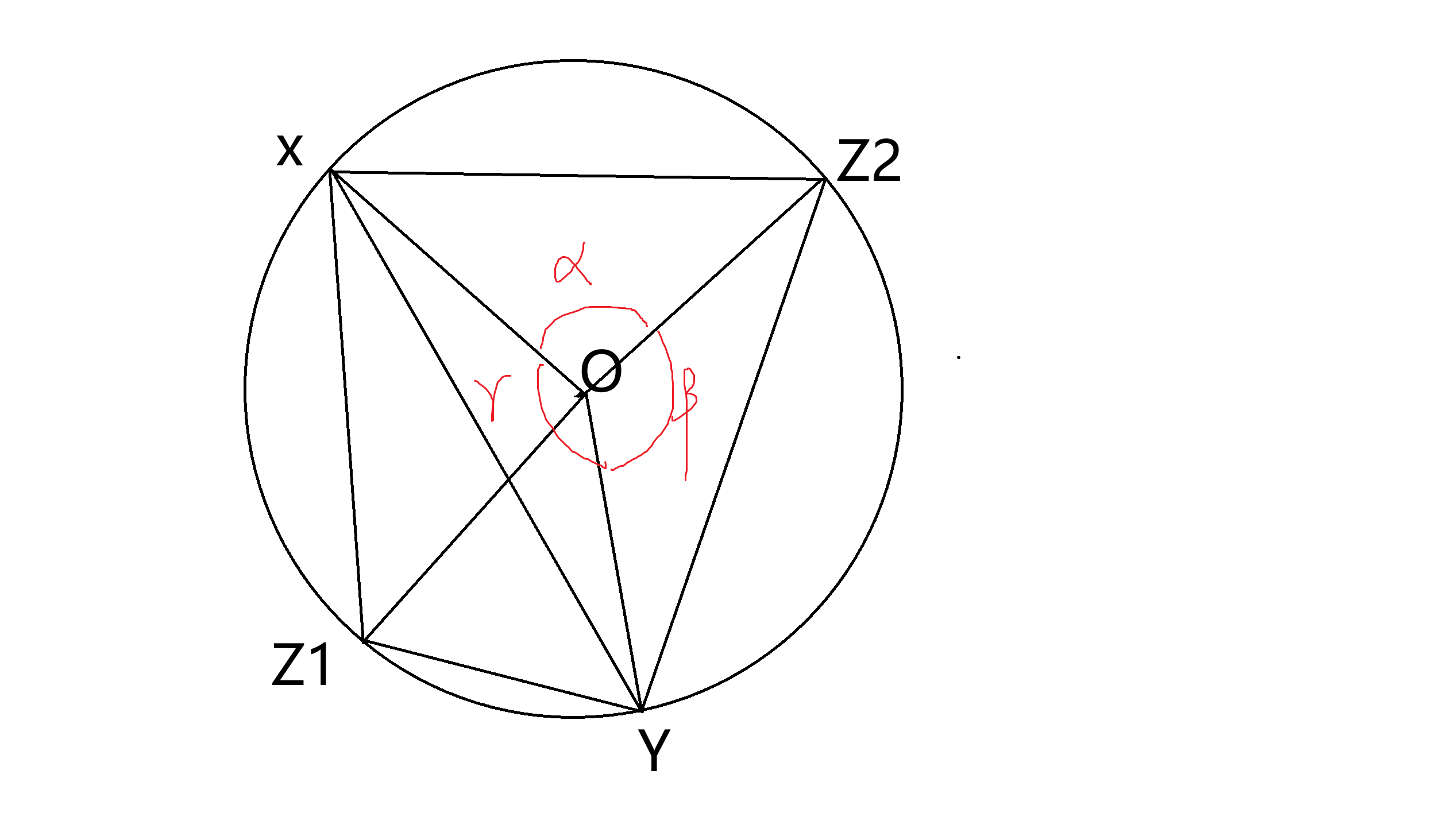
\[S_{\triangle X,Y,Z_2}=S_{\triangle X,Y,O}+S_{\triangle X,Z_2,O}+S_{\triangle Y,Z_2,O} \\
=\frac 1 2 XO \times YO \times \sin(\gamma) + \frac 1 2 XO \times Z_2O \times \sin(\alpha) + \frac 1 2 \times YO \times Z_2O \times \sin(\beta)
\]
枚举 \(X,Y,Z\) 即可做到 \(O(n^3)\)。
发现可以拆贡献,考虑固定下 \(X,Y\),对于 \(Z_1\) 这样的点,在计算 \(S_{\triangle X,Y,Z_1}\) 时 \(\triangle X,Y,O\) 给出负贡献,同理算 \(Z_2\) 时正贡献。
对所有极坐标 \(\theta\) 排序后,前缀和优化即可计算,时间复杂度 \(O(n^2)\),空间复杂度 \(O(n)\)。
发现时间对了,但是空间不对,将军的恩情!!!
这时想想数据范围是不是可能是“假的”,这应该是一个常用套路(有些题某个值太大 / 太小时答案没有含义,是固定的。)
看到给出的 \(\theta\) 是精确到 2 位小数,只有 36000 可能性。
考虑映射,将每个 \(\theta\) 映射到 \([0,36000)\) 的数上,就可以优化空间。
也可以通过观察大数据,发现大量重复得出。
但是时间不太对,发现精度限制很宽,所以映射到 \([0,3600)\) 也能过。
赛时我理解错误相对误差的含义,本身是 \(\frac {\Delta} {ans}\),理解成 \(|ans - myans|\),调高阈值喜提 \(100 \to 85 \to 15\)。
代码
link
#include<bits/stdc++.h>
#include<cmath>
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
typedef unsigned int ui;
#define rep(i, l, r) for(int i = l; i <= r; i++)
#define per(i, l, r) for(int i = l; i >= r; i--)
inline ll read(){ll res = 0, flg = 1;char c = getchar();for(; c > '9' || c < '0'; c = getchar()) if(c == '-') flg = -flg;for(; c >= '0' && c <= '9'; c = getchar()) res = res * 10 + c - '0';return res * flg;
}
template <typename T> inline void write(T x, char c = '\n'){if(x < 0) putchar('-'), x = -x;static int sta[35]; int top = 0;do { sta[top++] = x % 10, x /= 10; } while (x);while (top) putchar(sta[--top] + 48);putchar(c);
}
void __deb__(const char *s) { cerr << '\n'; }
template <typename T, typename... Ts>
void __deb__(const char *s, T v, Ts... vs){const char *c = strchr(s, ',');string name(s, c ? c - s : strlen(s));cerr << name << " : " << v;if(c) { cerr << " | "; __deb__(c + 1, vs...); }else cerr << '\n';
}
#define deb(...) __deb__(#__VA_ARGS__, __VA_ARGS__)
template <typename T> void chkmx(T &a, T b) { a = (a > b) ? a : b; }
template <typename T> void chkmn(T &a, T b) { a = (a < b) ? a : b; }
template <typename T> T calc_mod(T x, T mod){ while(x < 0) {x += mod;} x %= mod; return x; }
template <typename T> void mod_plus(T &x, T y, T mod) { x = calc_mod(calc_mod(x, mod) + calc_mod(y, mod), mod); }
template <typename T> void mod_sub(T &x, T y, T mod) { x = calc_mod(calc_mod(x, mod) - calc_mod(y, mod), mod); }
const int N = 36005;
const long double PI = 3.141592653589793238;
int n;
int cnt[N], sum[N];
const int rate = 10;
long double calc_sin(int x){return sin((double)x * PI / (180 * rate));
}
void solve_test_case(){cin >> n;double p;rep(i, 1, n){cin >> p;cnt[(int)(p * rate)]++;sum[(int)(p * rate)]++;}rep(i, 1, 360 * rate - 1){sum[i] += sum[i - 1];}long double ans = 0.0000000;int delta = 0;rep(i, 0, 360 * rate - 1){rep(j, i + 1, 360 * rate - 1){if(!cnt[i] || !cnt[j]) continue;delta = n - sum[j] + (i > 0 ? sum[i - 1] : 0) - (sum[j - 1] - sum[i]);ans += (double)delta * (calc_sin(j - i)) / 2 * cnt[j] * cnt[i];// deb(i, j, delta, ans);}}cout << fixed << setprecision(10) << ans / 1e10;
}
signed main(){ios::sync_with_stdio(0);cin.tie(0), cout.tie(0);// circ.in, circ.out// freopen("circ.in", "r", stdin);// freopen("circ.out", "w", stdout);int Test_case_num = 1;while(Test_case_num--) solve_test_case();return 0;
}
