ActiveMQ 默认是不启用认证的
但项目实施是必须需要用户名密码验证的,所以下面写下如果配置ActiveMQ用户名密码和开启认证
第一步、编辑ActiveMQ的登录配置文件
/opt/activemq/conf/jetty-realm.properties #或 /opt/activemq/conf/users.properties
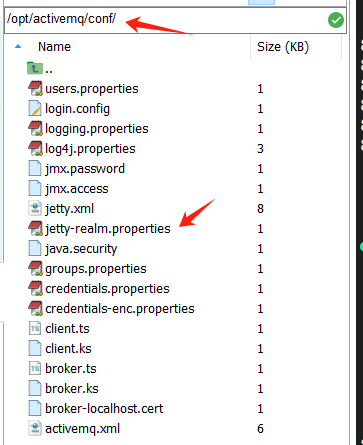
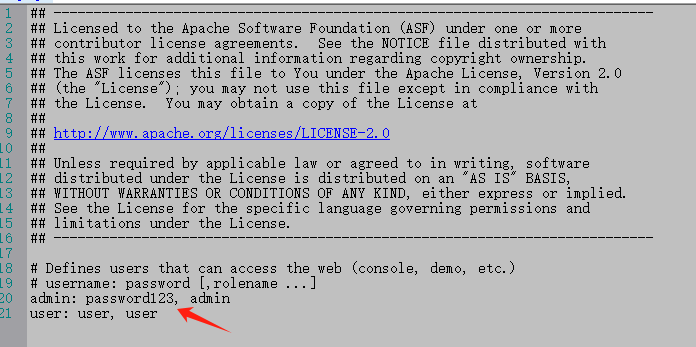
这里表示 用户名:admin 密码: password123
这个配置修改后需要重启ActiveMQ ,再用网页登陆则需要输入这个用户名密码了。
第二步、配置ActiveMQ的认证插件
编辑ActiveMQ配置文件 activemq.xml
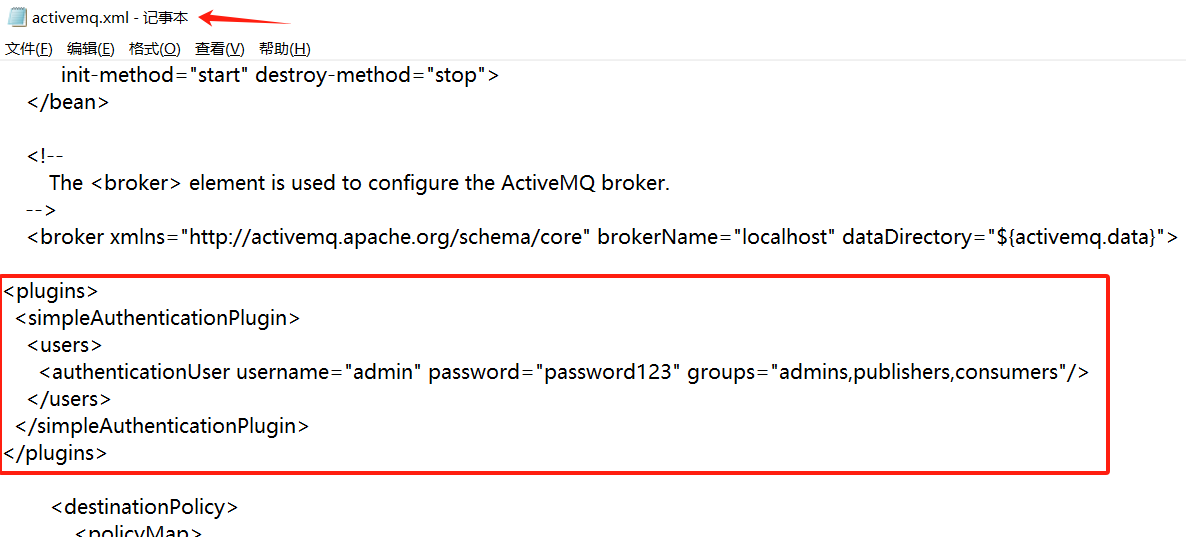
在<broker>标签内添加或修改认证插件配置:
<plugins><simpleAuthenticationPlugin><users><authenticationUser username="admin" password="password123" groups="admins,publishers,consumers"/></users></simpleAuthenticationPlugin> </plugins>
第三步、重启ActiveMQ服务使更改生效
sudo systemctl daemon-reload # 强制重载systemd配置 sudo systemctl restart activemq #重启服务

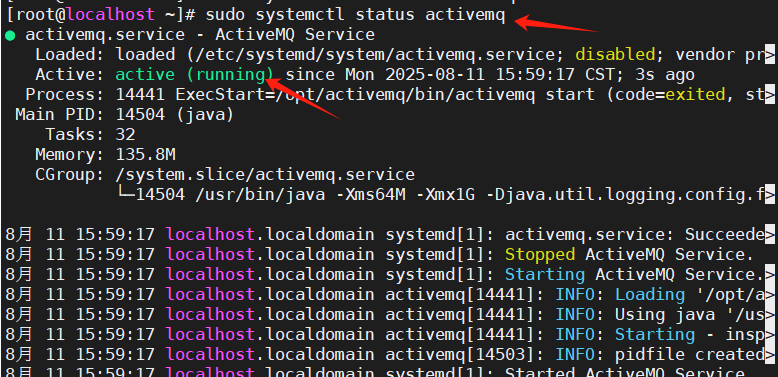
查看 ActiveMQ 运行状态
sudo systemctl status activemq
第四步、调整 Java 代码
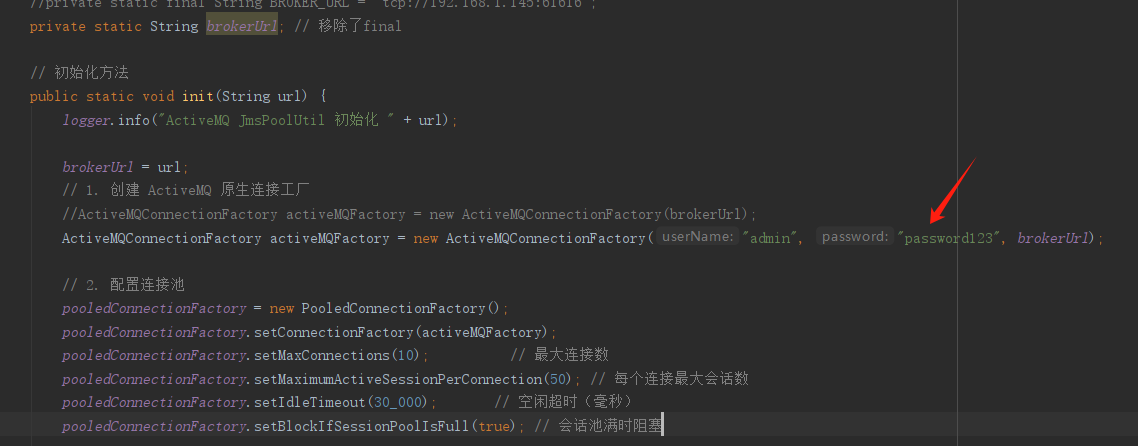
就改这一句即可
下面是完整代码
JmsPoolUtil.java
package com.JoinCallCCActiveMQToDM.ActiveMQ;import org.apache.activemq.ActiveMQConnectionFactory; import org.apache.activemq.jms.pool.PooledConnectionFactory; import org.slf4j.Logger; import org.slf4j.LoggerFactory;import javax.jms.*;public class JmsPoolUtil {protected static final Logger logger = LoggerFactory.getLogger(JmsPoolUtil.class);private static PooledConnectionFactory pooledConnectionFactory; //final//private static final String BROKER_URL = "tcp://192.168.1.145:61616";private static String brokerUrl; // 移除了final// 初始化方法public static void init(String url) {logger.info("ActiveMQ JmsPoolUtil 初始化 " + url);brokerUrl = url;// 1. 创建 ActiveMQ 原生连接工厂//ActiveMQConnectionFactory activeMQFactory = new ActiveMQConnectionFactory(brokerUrl);ActiveMQConnectionFactory activeMQFactory = new ActiveMQConnectionFactory("admin", "password123", brokerUrl);// 2. 配置连接池pooledConnectionFactory = new PooledConnectionFactory();pooledConnectionFactory.setConnectionFactory(activeMQFactory);pooledConnectionFactory.setMaxConnections(10); // 最大连接数pooledConnectionFactory.setMaximumActiveSessionPerConnection(50); // 每个连接最大会话数pooledConnectionFactory.setIdleTimeout(30_000); // 空闲超时(毫秒)pooledConnectionFactory.setBlockIfSessionPoolIsFull(true); // 会话池满时阻塞 }public static Connection getConnection() throws JMSException {return pooledConnectionFactory.createConnection();}public static void shutdown() {pooledConnectionFactory.stop();} }
