官方题解搬运工。
题意:给你一个环,长度为 \(M\),点有容量 \(C_i\),要求出这个环的最大匹配,同时会有 \(q\) 次询问,每次询问修改一个 \(C_i\),求最大匹配。
做法:
首先我们记 \(B_i = \min(C_i+1,C_i)\),这里 \(C_{0} = C_{M}\),那么我们重新刻画这个问题为找一组 \(x\),代表第 \(i,i+1\) 个点之间的边的匹配量,有的限制是:
\[x_i\le B_i,x_i+x_{i+1}\le C_i
\]
其实你会发现后者的限制其实比较多余,但是这跟我们后面的做法有关。
我们讨论一下环长 \(M\) 的奇偶性。
- \(M\) 为偶数。
我们考虑建立如下的网络流,这里以 \(M=6\) 为例:
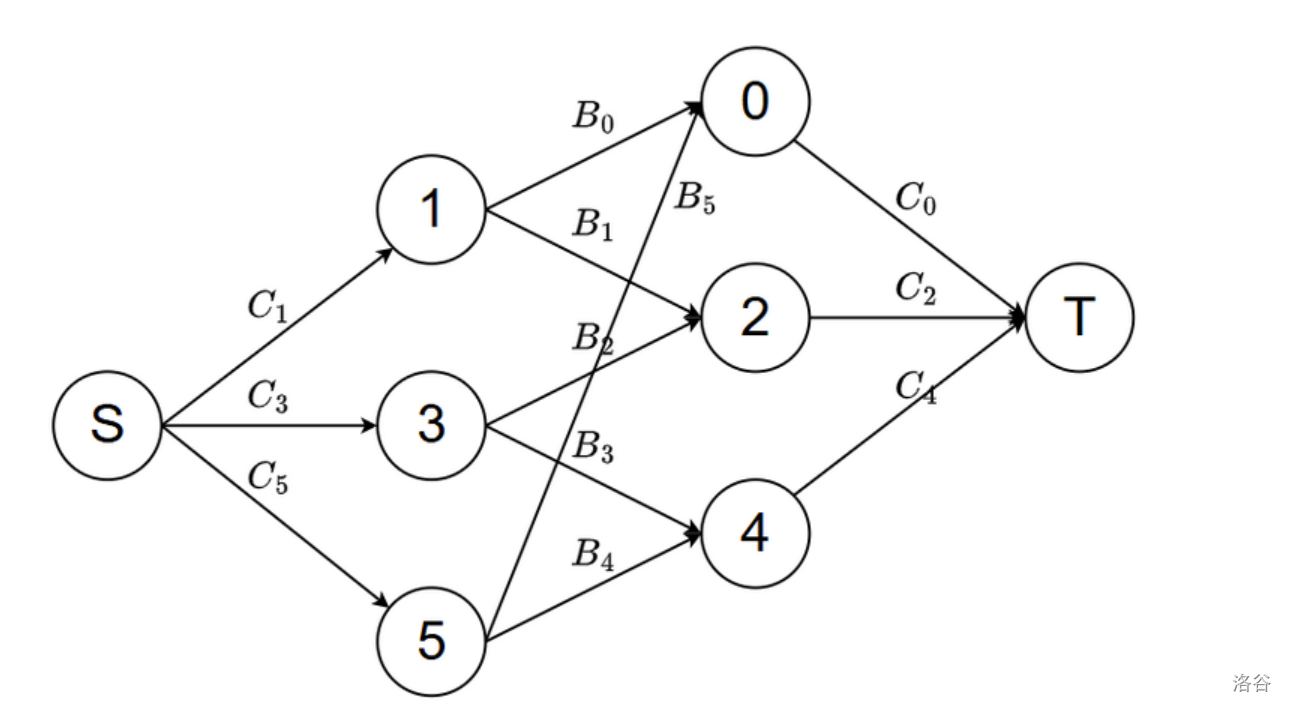
那么显然这个图的最大流就是答案。
我们考虑把最大流转换为最小割,因为这里的限制都只和 \(i-1,i+1\) 有关,所以我们很自然地想到设 \(dp_{l,r,0/1,0/1}\) 代表区间 \([l,r]\) 左端点和右端点他们到源/汇的边是否被割,显然采用线段树加速,转移时讨论 \(mid,mid+1\) 是否被割来决定中间是否要割 \(mid \rightarrow mid+1\) 这条边。
- \(M\) 为奇数。
现在我们仍然考虑建出一个和上面一样的网络流,这里以 \(M=5\) 为例:
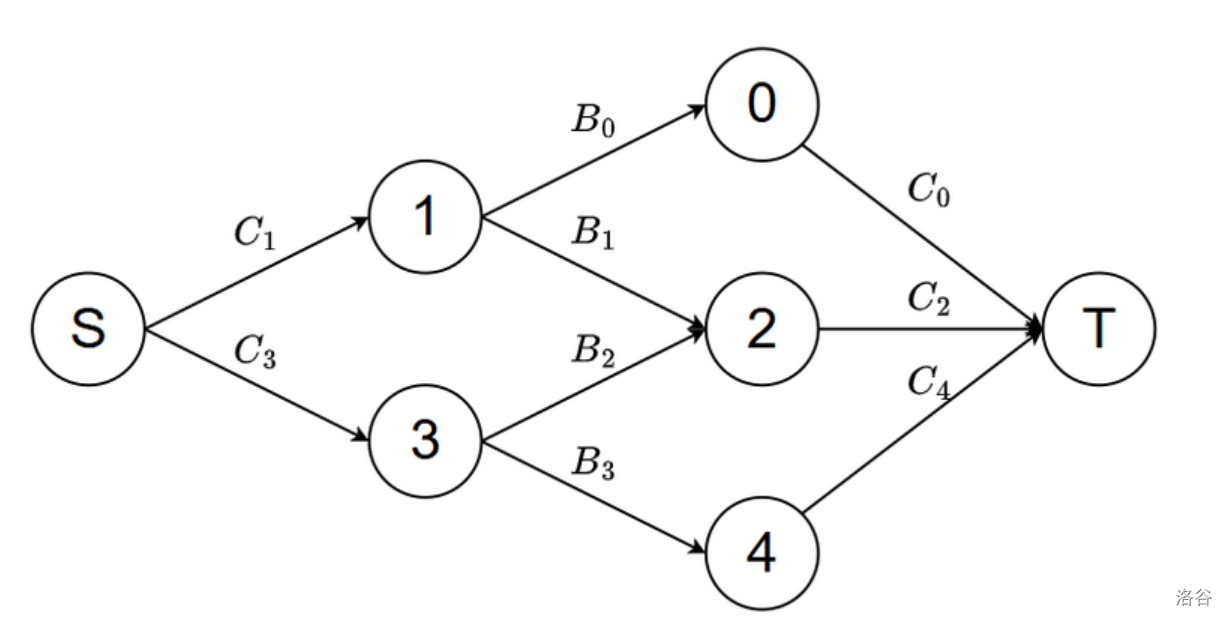
但是我们发现一个问题,\((0,M-1)\) 的限制没有被加到这个图里面,我们之前的做法完全爆了。
我们考虑一个暴力的想法,我们直接枚举 \(x_{M-1}\) 用了多少个,然后直接把 \(C_0\) 和 \(C_{M-1}\) 减去这么多,变成这个图:
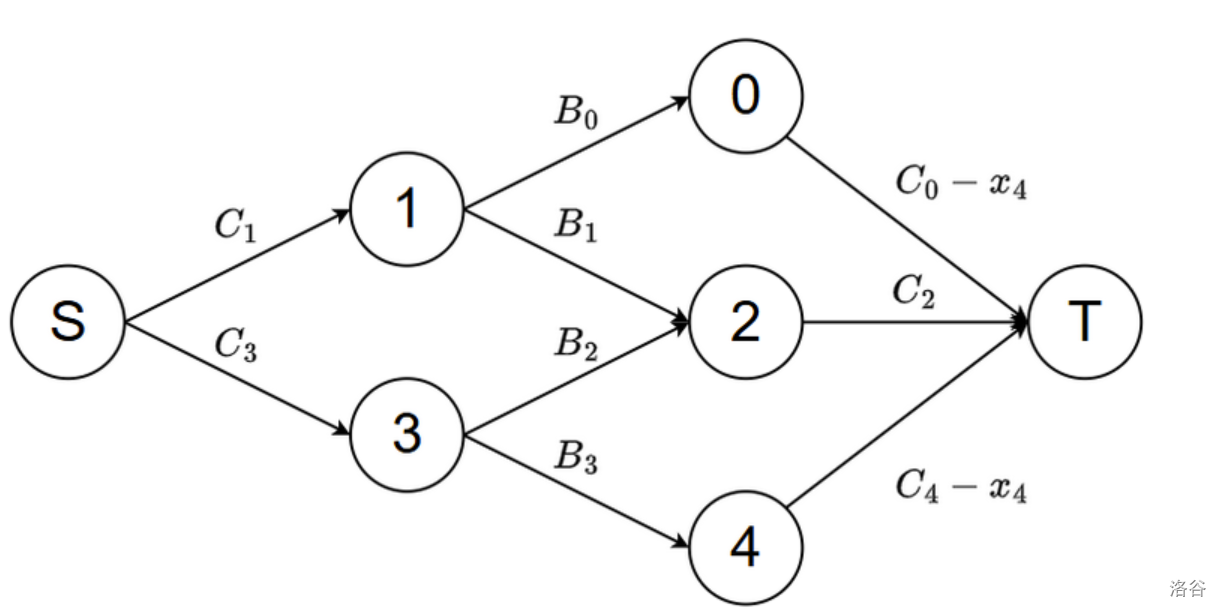
这个图就可以用我们上面的做法了。
注意到 \(x_{M-1}\) 其实只会影响到 \(0,M-1\) 这两个地方,所以他其实是一个三段的分段函数,直接分段维护即可。
