Luogu题解：P13427 [COCI 2020/2021 #2] Odasiljaci

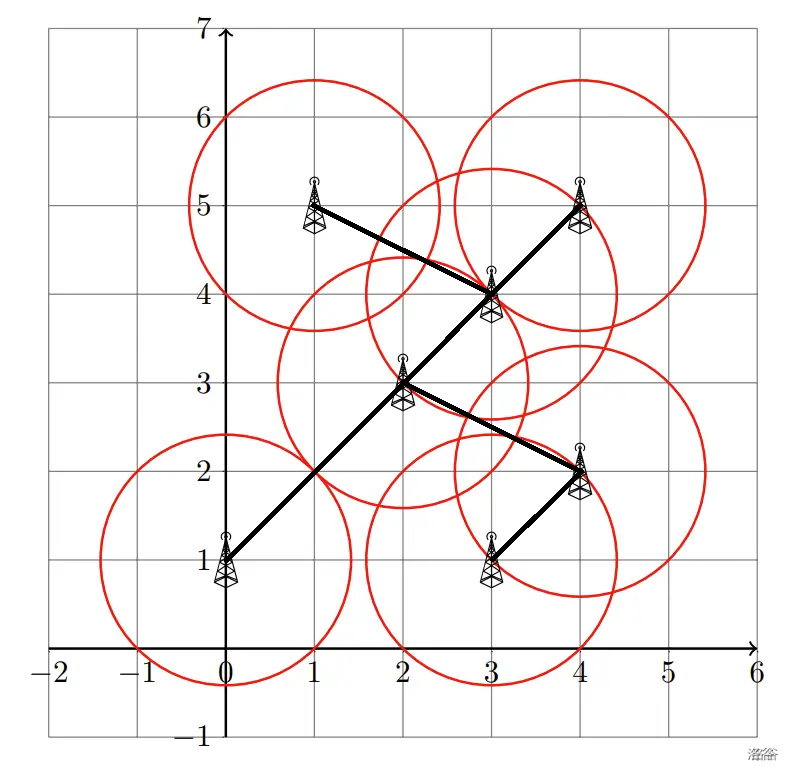
题意

题意也是很简单，就是找一个距离\(n\)，其中\(x\times2\)可以将每一个信号塔连接起来，并输出最小的\(n\)。

解释：

Q：为什么是用\(x\times2\)的距离就可以连起来？

A：因为信号在过了两个信号塔距离的一半，就会被另一个信号塔接收到。

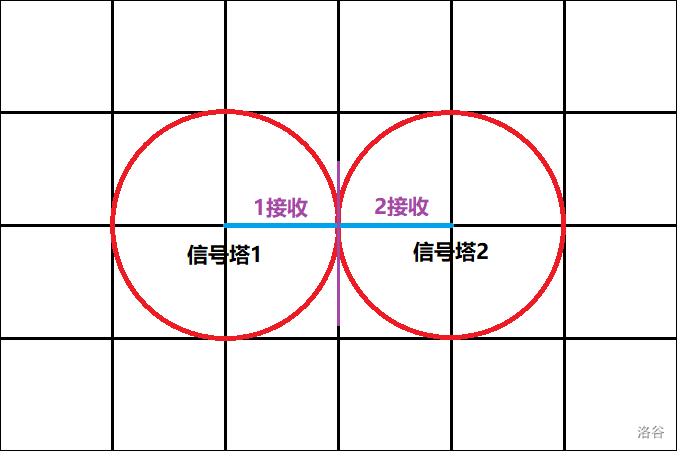
注意： 不一定要直接相连，可以\(x_1\)连接\(x_2\)，\(x_2\)连接\(x_3\)。

思路

1. 将每一个信号塔找到离它最近的信号塔找到，将所有信号塔连成一串。如图：
   
2. 再将每条线段的一半算出来，求出最大值并输出。

代码

#include<bits/stdc++.h>
using namespace std;
const int N = 1005;
struct node{int x, y;
}arr[N];
double dis(node a, node b){return sqrt(pow(a.x - b.x, 2) + pow(a.y - b.y, 2));
}
struct edge{int u, v;double d;
}e[N * N];
int cnt;
bool cmp(edge a, edge b){return a.d < b.d;
}
int father[N];
void init(){for(int i = 1; i < N; i++)father[i] = i;
}
int find(int x){if(x != father[x])x = find(father[x]);return father[x];
}
bool bing(int a, int b){int x = find(a);int y = find(b);if(x != y){father[y] = father[x];return 1;}return 0;
}
double kruskal(int p, int s, int t){init();double sum = 0;int cnt = 0;for(int i = 0; i < t; i++){if(bing(e[i].u, e[i].v)){cnt++;sum = max(sum, e[i].d);if(cnt == p - 1){return sum;}}}return 0;
}
int main(){int s, q;cin >> q;for(int i = 1; i <= q; i++){cin >> arr[i].x >> arr[i].y;} for(int i = 1; i <= q; i++){for(int j = i + 1; j <= q; j++){e[cnt++] = {i, j, dis(arr[i], arr[j])};}}sort(e, e + cnt, cmp);cout << fixed << setprecision(7) << kruskal(q, s, cnt)/2;return 0;
}